فهرست مطالب

نقش نمودار CUSUM در ارتقاء کنترل کیفیت

از شناسایی تغییرات کوچک تا بهبود فرآیندهای بالینی

مقدمه

در دنیای پیچیده آزمایشگاه‌های بالینی، کنترل کیفیت به عنوان یکی از ارکان اساسی بهبود کارایی و دقت نتایج تخصصی پزشکی محسوب می‌شود. یکی از ابزارهای نوآورانه در این زمینه، نمودار Cusum است که به منظور ارتقاء و تضمین کیفیت فرآیندهای آزمایشگاهی طراحی شده است Cusum با فراهم‌سازی یک مدل ساختاریافته برای تجزیه و تحلیل داده‌ها، نه تنها امکان شناسایی نقاط قوت و ضعف در فرآیندهای آزمایشگاهی را فراهم می‌آورد، بلکه با تطبیق سریع با تغییرات و به روزرسانی‌های مورد نیاز، باعث افزایش سطح اعتماد و اعتبار نتایج آزمایشگاهی می‌شود. در این مقاله، به بررسی ساختار، اهمیت و کاربردهای این ابزار مهم در کنترل کیفیت آزمایشگاه‌های بالینی خواهیم پرداخت.

معرفی:

Cusum، یا نمودار کنترلی تجمعی، یک تکنیک آماری برای نظارت بر تغییرات فرآیندها است. این روش به منظور تشخیص تغییرات کوچک در میانگین فرآیند یا تغییراتی که ممکن است در طول زمان رخ دهند، توسعه یافته است. برخلاف روش‌های سنتی کنترل کیفیت که بر اساس مشاهدات فردی عمل می‌کنند، Cusum از تجمیع تفاوت‌های مقداری مشاهده شده از مقدار هدف یا میانگین استفاده می‌کند، و این امر باعث شناسایی سریع‌تر و دقیق‌تر ناهنجاری‌ها می‌شود. این ویژگی Cusum را به ابزاری قدرتمند برای کاربرد در محیط‌هایی با نیاز به دقت بالا، مانند آزمایشگاه‌های بالینی، تولیدات صنعتی حساس و در صنایع دارویی، تبدیل کرده است. Cusum نه تنها در شناسایی سریع تغییرات ناگهانی مفید است، بلکه با ارائه یک نمای کلی از پایداری فرآیند، در بهبود کلی کیفیت و کاهش هزینه‌های ناشی از محصولات معیوب نیز نقش مهمی ایفا می‌کند.

تاریخچه ی پیدایش:

CUSUM یا “Cumulative Sum Control Chart” یکی از ابزارهای کنترل کیفیت آماری است که برای شناسایی تغییرات کوچکی که ممکن است در فرآیند تولید یا خدمات رخ دهد، طراحی شده است. این روش اولین بار توسط ای.اس. پیج (E. S. Page) در دهه ۱۹۵۰ معرفی شد و به دلیل توانایی در تشخیص سریع تغییرات ناپیوسته در میانگین فرآیند، به‌ویژه تغییرات کوچک، محبوبیت یافت.

Cusum در طول زمان توسعه یافته و بهبود یافته است تا شامل کاربردهای متنوعی در صنایع مختلف و برای تحلیل داده‌های پیچیده‌تر شود. به عنوان یک ابزار قدرتمند در مجموعه ابزارهای کنترل کیفیت، Cusum همچنان به‌عنوان یک روش استاندارد برای پایش فرآیندها و تضمین کیفیت شناخته می‌شود.

خطای سیستماتیک:

خطایی که الگو و جهت خاصی دارد و در تکرار اندازه گیری ها هم چنان تکرار می گردد.

خطای سیستماتیک با تکرار اندازه گیری یا افزایش حجم نمونه کاهش نمی یابد.

نام دیگر این نوع خطا سوگرایی، تورش یا Bias است و مقدار آن با محاسبه میانگین نتایج حاصل از انجام تعداد نامحدودی اندازه گیری یک اندازه در شرایط تکرارپذیر منهای مقدار واقعی آن اندازه تعیین می گردد.

خطای سیستماتیک از روش های ناقص، تجهیزات کالیبر نشده یا برخی از متغیرها که نتیجه اندازه گیری را هر بار با مقدار ثابتی تغییر می دهند، ناشی می شود. خطای سیستماتیک می تواند شناخته یا ناشناخته باشد. یک خطای سیستماتیک معلوم یا معین، نامیزانی یا bias نامیده می شود.

مثال:

عوض کردن معرف بدون تغییر کالیبراسیون
تخریب تدریجی معرف
عدم رعایت دستورالعمل سازنده برای تهیه معرف

نحوه ی رسم نمودار:

روشی است که جمع جبری اختلاف نتایج آزمایش نمونه کنترل را با میانگینی که در ابتدا تعیین شده است، بررسی می نماید و به خطاهای سیستماتیک حساس است. در شرایط معمول، نتایج کنترل ها در اطراف میانگین بالاتر و پایین تر قرائت می شوند؛ اما اگر نتایج سیر نزولی یا صعودی پیدا کنند، جمع جبری اختلافات نتایج با میانگین، افزایش یافته و احتمال بروز خطای سیستماتیک مطرح می شود. برای اجرا و تفسیر چارت Cusum دو راه وجود دارد:

روش v-mask
محدوده تصمیم گیری Decision-Limit

از آنجائيكه روش محدوده تصميم گيري ،(decision limit) ساده تر بوده و قابليت اجراي كامپيوتري نيز دارد؛ در اين مقاله راجع به اين روش توضيح داده مي شود.

رسم نمودار Cusum به روش Decision Limit

کنترل را 20 بار آزمایش کرده، میانگین و انحراف معیار آن را محاسبه نمایید.
نمودار کنترلی را ترسیم نمایید که در آن محور y نشانگر Cusum با خط مرکزی صفر باشد.
باید دو محدوده را مشخص نمایید.
و به اندازه Mean±1SD در نظر گرفته می شود و و که محدوده کنترل است و برابر 7SD± در نظر گرفته می شود.
در هر سری کاری یک نمونه کنترل آزمایش و نتیجه آن را با محدوده Mean±1SD مقایسه کنید تا زمانی که نتیجه خوانده کنترل در این محدوده قرار دارد، Cusum اجرا نمی شود و در این مرحله علامت گذاری بر روی نمودار انجام نمی شود.
به محض اینکه کنترل از محدوده Mean±1SD خارج شد، اختلاف نتیجه مشاهده شده را با یا محاسبه نمایید. بدین صورت که اگر مقدار خوانده کنترل بیشتر از باشد، اختلاف خوانده کنترل از و اگر خوانده کنترل کمتر از باشد، اختلاف خوانده کنترل از محاسبه می شود.

مثال:پایش کیفیت تری گلیسیرید در سرم کنترل

داده اولیه:

Mean : 100mg/dl

انحراف معیار 𝜎)(: 5mg/dl

محاسبه انحراف استاندارد شده (Z) :

فرض کنید مقدار مشاهده شده طی روزهای متوالی

110,100,108,105,105,101,96,105,101,101,111,102,110,107,107,107 باشد.

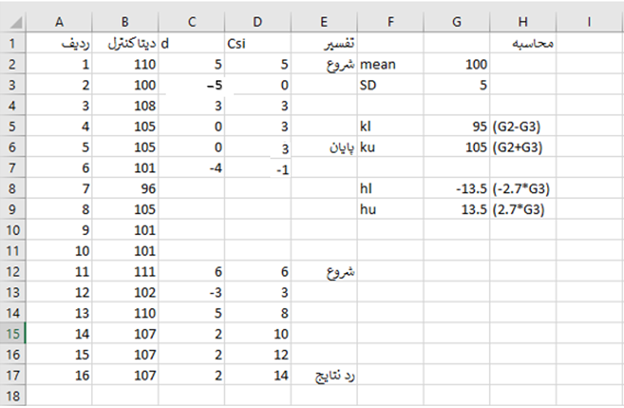
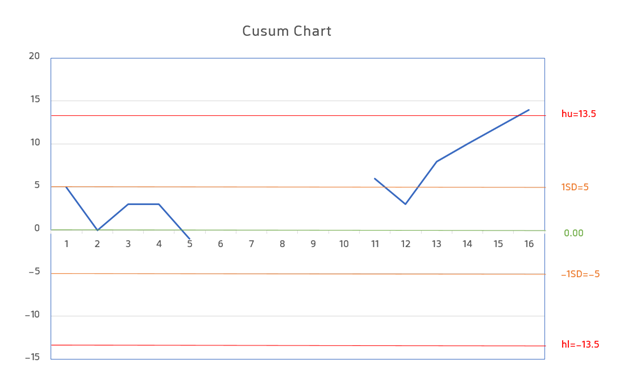
در هر سری عدد حاصل از اختلاف خوانده کنترل از مقادیر K با مقادیر بالاتر از خود جمع می شود و به عنوان داده جدید برای همان خوانده کنترل محاسبه می شود و بر روی نمودار ثبت می شود. پایان حذف خطای سیستماتیک در دو حالت اتفاق می افتد:

جهت منحنی عوض شود. یعنی علامت جبری از مثبت به منفی یا برعکس، از منفی به مثبت تغییر یابد، که در این حالت شرایط تحت کنترل قرار گرفته است.
مقدار جمع جبری از کمتر و یا از فراتر رود، که در این حالت شرایط از کنترل خارج شده است. و سری کاری باید تا شناسایی و حذف خطای سیستماتیک متوقف شود.

نمودار CUSUM (Cumulative Sum Control Chart) و نمودار Levey-Jennings هر دو ابزارهای کنترل کیفیت آماری هستند، اما برای مقاصد و موقعیت‌های مختلف استفاده می‌شوند. به مقایسه ی این دو با هم می پردازیم:

نمودار CUSUM

هدف:
- برای شناسایی تغییرات کوچک و مداوم در فرآیند استفاده می‌شود. هنگامی که می‌خواهید تغییرات تدریجی که نمودارهای کنترل استاندارد نمی‌توانند شناسایی کنند را پیدا کنید، نمودار CUSUM مؤثرتر است.

روش کار:
- این نمودار انحراف‌های هر نقطه داده از مقدار هدف را جمع می‌کند و مجموع تجمعی این انحراف‌ها را نمایش می‌دهد.
ویژگی‌ها:
- حساسیت بالا به تغییرات کوچک.
- معمولاً به یک خط مرکزی و خطوط هشدار یا کنترل نیاز دارد.

نمودار Levey-Jennings

هدف:
- بیشتر در کنترل کیفی آزمایشگاهی و برای ارزیابی و نمایش نتایج آزمون‌های کیفی در طول زمان استفاده می‌شود.
روش کار:
- نتایج اندازه‌گیری‌های حاصل از آزمون‌های کیفی را بر اساس انحراف معیار واحد بر روی نمودار نشان می‌دهد.
ویژگی‌ها:
- دارای خط میانی و معمولاً خطوط مربوط به انحراف استاندارد (±1، ±2 و ±3 انحراف معیار) است.
- برای ارزیابی پایداری نتایج آزمایشگاهی به کار می‌رود.